Properly doing cameras interpolation through a target (II)
This is the 2nd post on the series Properly doing cameras interpolation through a target:
Having fun interpolating cameras? Let's take a look at some issues of the Camera interpolator we started on the previous post and fix them
The Rotation issue
If you test the interpolator a little bit you'll see it behaves very well even with moving objects. Because it focuses on the target it doesn't matter if it is moving or not, on any step of the interpolation it places itself on the target position and then interpolates from there.
But there is an issue interpolating between rotating cameras. Make the target rotate by adding the next script to it
and then set any of your cameras as children of the target so they rotate with them. Now pay attention to what happens when you interpolate from this camera to itself:
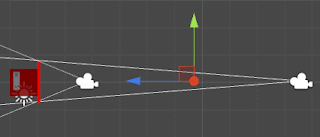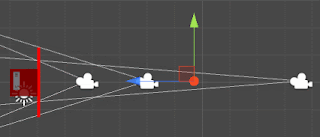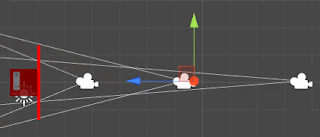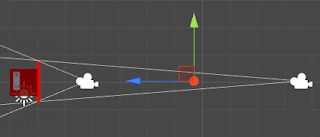
It actually seems as if the camera were moving forwards and then backwards. Why is this happening? Take a look at how the height of the camera on the target position (marked in red) is currently being interpolated:
The height is actually growing and then shrinking instead of being kept constant. This happens because interpolating the fov linearly doesn't actually make the height being interpolated linearly too (If one of the angles of a triangle grows 50% that doesn't make the opposite side grow by 50%)
There are two ways to solve this: we have to interpolate the height first and then we could either interpolate the fov and then calculate the local z or we could interpolate the local z and then calculate the fov. In my experience interpolating the fov looks smoother and is bit more friendly to the eye, so we'll go for that option. The three parameters (fov, height and local z) are connected like this
This is what happens if you just interpolate the fov and then calculate the local z:
as you can see the height is kept constant (marked with the red line) but now the near and far values are the ones moving (in this case there is an instant where the target is actually not being rendered). This is because the z now is not moving linearly and because the near and far values are relative to this z they are displaced. We need to interpolate the near and far values with the same t used for the z. The way to calculate this t is
But there is an issue interpolating between rotating cameras. Make the target rotate by adding the next script to it
and then set any of your cameras as children of the target so they rotate with them. Now pay attention to what happens when you interpolate from this camera to itself:
instead of staying still it does a little annoying movement. This doesn't happen if you stop the rotation. The reason why this is happening is because we are interpolating the rotation in world space, and because the target is rotating this value is changing every frame and so an interpolation appears. So how should we store the rotation then? There are 3 possibilities:
- Relative to cameraFrom
- Relative to the target (same as the position)
- Relative to the cameraTo
we have already seen why it is not a good idea to keep things relative to cameraFrom, so let's focus on the other two. At first one could think that since we are already keeping the position relative to the target then it would be a good idea to do the same with the rotation, but no. In a few cases where I have tested cameras interpolation, the target tends to continue rotating after changing its camera (a car on a curve for example) and that gives a weird sensation because everything rotates around it if we attach a camera directly. Instead the camera we are interpolating to is a camera that is prepared to handle the movement of the target (it will continue being the main camera after the interpolation) so it looks like a much better candidate. This is mostly based on experience so if I don't convince you then you should experience it by yourself (and let me know your thoughts).
So, yeah, we are gonna keep the rotation relative to the camera target. The good thing about this is that the end rotation will always be the identity (since the identity rotation relative to the camera target is the rotation of the camera itself). And the way to calculate one rotation in Unity relative to another is by doing
relativeRot = Quaternion.Inverse(referenceRotation) * worldRotation
changin just lines 56 and 83 we have the problem solved
The Fov interpolation issue
The current interpolator not only interpolates position and rotation, but also the parameters of the camera: fov, near and far. There is an interesting issue with the way we are interpolating the fov. In order to see it, place two cameras with different fovs in the same position and displace them in their local z so that they render the target in a similar screen position. This is what happens when you interpolate between them:It actually seems as if the camera were moving forwards and then backwards. Why is this happening? Take a look at how the height of the camera on the target position (marked in red) is currently being interpolated:
The height is actually growing and then shrinking instead of being kept constant. This happens because interpolating the fov linearly doesn't actually make the height being interpolated linearly too (If one of the angles of a triangle grows 50% that doesn't make the opposite side grow by 50%)
There are two ways to solve this: we have to interpolate the height first and then we could either interpolate the fov and then calculate the local z or we could interpolate the local z and then calculate the fov. In my experience interpolating the fov looks smoother and is bit more friendly to the eye, so we'll go for that option. The three parameters (fov, height and local z) are connected like this
This is what happens if you just interpolate the fov and then calculate the local z:
float tZ = (z - z0) / (z1 - z0);
where z was calculated based on the fov interpolation and z0, z1 the initial and final values. Also we need to make sure that z1 and z0 are different to avoid a divission by zero, if that happens we just need to use the same t used for the fov interpolation (there is no displacement on z, so near and far won't be displaced). Now if we used this tZ to interpole near and far we get this:
And this is how the Refresh function should look like:
Orthographic Cameras
So far we have been interpolating between cameras using perspective. But there is another type of cameras available in Unity by default (and is also a type of Cameras very common in videogames).
Instead of a fov, in Unity, orthographic cameras are defined by an orthographic size which according to the documentation represents half of the screen height. Also, orthographic cameras have their projection lines parallel between them. Although they look very different at first it is posible to create a perspective camera that looks very similar to an orthographic one, and this is the trick we are gonna use to interpolate to and from them.
On a perspective camera the lower the fov the more parallel the projection lines become. They will become parallel at infinity but we don't need to go that far to make an interpolation that looks good. We have already seen a way to keep the height constant while interpolating the fov. Now take a look at what happens when we pick a perspective Camera and interpolate its fov to 0,1 (and then calculate its local z)
It's not orthographic at the end, but close to, and good enough for an interpolation. We need to do this conversion in three different parts of the code:
- At the beggining of the interpolation, if the previous one is finished, to retrieve the current values of the previous camera
- At the beginning of the interpolation, on CameraFrom
- Every Frame, on CameraTo (since it could be moving)
Because of this I ended up creating a small internal class CameraParams that stores all the info and also manages the conversion. The code with all the changes is the next one
It's not orthographic at the end, but close to, and good enough for an interpolation. We need to do this conversion in three different parts of the code:
- At the beggining of the interpolation, if the previous one is finished, to retrieve the current values of the previous camera
- At the beginning of the interpolation, on CameraFrom
- Every Frame, on CameraTo (since it could be moving)
Because of this I ended up creating a small internal class CameraParams that stores all the info and also manages the conversion. The code with all the changes is the next one
Avoid Linear interpolation
We are almost done. Just a small tweak to improve the script a lot. So far we have been using a linear interpolation (getting t from interpolationTimeAccum / interpolationTime). Linear interpolations in videogames always look bad, you should avoid them at all cost in order to make things feel more natural.
Luckily in Unity it is very easy to add curves using the type AnimationCurve, and then we just need to change this
float t = interpolationTimeAccum / interpolationTime;
into this
float t = interpolationCurve.Evaluate(interpolationTimeAccum / interpolationTime);
you can find the final script here
Done
Pfiuuu! We are finally done. This is something I wanted to do for a long time. I am pretty happy with the result. I have tried to explain all the issues I saw when I finally sat down and coded it (and also my memory is really bad so having all this written here will be very helpful for me in the future).
You can of course skip it to the end and just grab the script and use it, it's up to you. I have shown you how to do this on Unity but if you understand it, it shouldn't be a problem to use it anywhere. As usual what really matters is the knowledge, not the language or the program you are using.
Please drop me some comments with your doubts of your opinion about the post, it makes me happy to read them :)
Happy camera coding!
You can of course skip it to the end and just grab the script and use it, it's up to you. I have shown you how to do this on Unity but if you understand it, it shouldn't be a problem to use it anywhere. As usual what really matters is the knowledge, not the language or the program you are using.
Please drop me some comments with your doubts of your opinion about the post, it makes me happy to read them :)
Happy camera coding!
Labels: cameras, interpolation, unity3d












5 Comments:
it's nice that you took the time to write all this. And your github source snippet thing does wonders ^_^
By PypeBros, at November 08, 2017 10:42 PM
PypeBros, at November 08, 2017 10:42 PM
This little piece of code is being very helpful to me. Glad you liked it :D
By Zalo, at November 09, 2017 9:44 AM
Zalo, at November 09, 2017 9:44 AM
ow about java program for detection color and puttext in open cv (eclipse) ?
I've tried with a java program in open cv for color detection, but for putText any problem .. *give text on object
May I know your email
By xcom2 cheats, at January 23, 2018 11:32 AM
xcom2 cheats, at January 23, 2018 11:32 AM
Hi, I follow exactly what you did and get following error:
NullReferenceException: Object reference not set to an instance of an object
OneThirdViewAngle.LateUpdate () (at Assets/Scripts/OneThirdViewAngle.cs:42)
By alternative to ziploc bags, at February 28, 2018 12:19 PM
alternative to ziploc bags, at February 28, 2018 12:19 PM
OneThirdViewAngle doesn't seem like any of the classes I am talking about in this tutorial
By Zalo, at February 28, 2018 1:34 PM
Zalo, at February 28, 2018 1:34 PM
Post a Comment
<< Home