Painting in 2D using 3D (II)
Ok, some people who read the previous post told me that they dindn't understand anything of what I was saying :D So I'll try to go explain everything a little bit more better this time. Let's just focus on the first issue I was talking about.
When you are painting on the screen and you are using a 3D Engine (like opengl) there is something called the pipeline. You just don't draw 2d vertices on the screen as usual, but in 3d. You are painting on 3d wether you like it or not. You can check this pipeline on the internet (here, for example http://june.ncviz.com/openglpipeline.html) Basically what goes on with a 3d vertex that you draw is that it is being transformed throught the pipeline until it is finally painted in 2d into the screen.
You can't avoid these transformations, all right? Let's focus on the first two steps of this pipeline. You define a vertex and it is first multiplied by the modelview matrix and then by the projection matrix (sometimes modelview martrix is divided into camera matrix and object transformation) and after that we don't care now (if you are interested read it in the previous link :D)

The first matrix transforms the vertex coordinates into view coordinates (still on 3d) and the second (which we are specially interested on) projects them on 3d according to the perspective we have defined. You usually define a 3d perspective with a frustrum (a truncated square pyramid). With thise kind of perspective closest objects are seen bigger than further ones
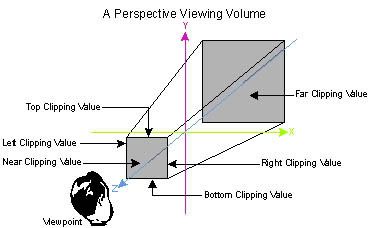
This is the way you paint on 3d. But there is also a special perspective known as orthographic in which the size of the objects doesn't depend on the distance to the camera. It doesn' matter how far they are you'll see them always the same. This kind of perspective is defined on OpenGl using glOrtho(). http://www.cs.utk.edu/~vose/c-stuff/opengl/glOrtho.html
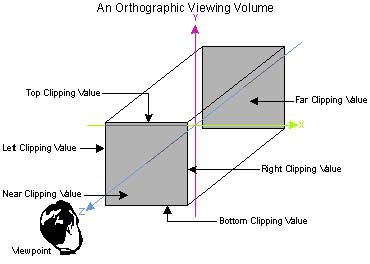
void glOrtho( GLdouble left,
GLdouble right,
GLdouble bottom,
GLdouble top,
GLdouble zNear,
GLdouble zFar )
Using glOrtho(0, SCREEN_WIDHT, 0, SCREEN_HEIGHT, 1, 0) we can say that you have created a full screen canvas. Now if you paint a vertex on (x, y, z) the point will be painted on the screen on (x, y) and z will define wich point goes behind the others. Easy!!
When you are painting on the screen and you are using a 3D Engine (like opengl) there is something called the pipeline. You just don't draw 2d vertices on the screen as usual, but in 3d. You are painting on 3d wether you like it or not. You can check this pipeline on the internet (here, for example http://june.ncviz.com/openglpipeline.html) Basically what goes on with a 3d vertex that you draw is that it is being transformed throught the pipeline until it is finally painted in 2d into the screen.
You can't avoid these transformations, all right? Let's focus on the first two steps of this pipeline. You define a vertex and it is first multiplied by the modelview matrix and then by the projection matrix (sometimes modelview martrix is divided into camera matrix and object transformation) and after that we don't care now (if you are interested read it in the previous link :D)

The first matrix transforms the vertex coordinates into view coordinates (still on 3d) and the second (which we are specially interested on) projects them on 3d according to the perspective we have defined. You usually define a 3d perspective with a frustrum (a truncated square pyramid). With thise kind of perspective closest objects are seen bigger than further ones

This is the way you paint on 3d. But there is also a special perspective known as orthographic in which the size of the objects doesn't depend on the distance to the camera. It doesn' matter how far they are you'll see them always the same. This kind of perspective is defined on OpenGl using glOrtho(). http://www.cs.utk.edu/~vose/c-stuff/opengl/glOrtho.html

void glOrtho( GLdouble left,
GLdouble right,
GLdouble bottom,
GLdouble top,
GLdouble zNear,
GLdouble zFar )
Using glOrtho(0, SCREEN_WIDHT, 0, SCREEN_HEIGHT, 1, 0) we can say that you have created a full screen canvas. Now if you paint a vertex on (x, y, z) the point will be painted on the screen on (x, y) and z will define wich point goes behind the others. Easy!!
